Review of Music Of The Primes

I've just finished a lovely, lovely book by Marcus du Sautoy on the history of the Reimann Hypothesis, one of the biggest problems in mathematics, ever...

..it's driven at least one person to madness, and taken a few to the borders.  It's the stuff that techno-thriller spy movies are made of (literally, see Sneakers) and has been implicated in at least one fatal duel and one national revolution.  It's been the subject of, and I kid you not, two Nobel Prize level practical jokes.

 Full review on my Cool Science Books blog...

P=NP? P!=NP? What The Hell Is That All About?

Firstly, an apology.  This is an attempt to explain, to the layman, something which I barely understand myself.  This might not work....apologies all round if it doesn't...

You may have heard that somebody recently submitted a proposed proof to the P=NP problem in maths.  The someone in question is  Vinay Deolalikar, a researcher at Hewlett Packard.  Whilst he developed the paper outside of company time he's still speaking within his field of expertise, this isn't just an obscure pure maths problem, it's one that has some very important consequences for virtually anyone who uses a computer these days.  That's you by the way, unless you're reading this on a printout, and kudos if you are.

The P=NP problem is, in plain English, about how long it takes to find the right answer when there's lots of answers.  It's all about a particular kind of problem, one that produces a lot of potential answers - the Travelling Salesman problem is a classic example.  Imagine you have to visit five different cities, you know the distances between each of them, and you want to visit every one of them, from any starting point, and travel the shortest distance possible.  

The obvious solution is to check every possible trip and find the shortest that way.  The number of possible trips is the number of cities (5) times the number of the next city you could visit, times the next....and so on.  "Five factorial" if you want the proper name for it, or "5!" in shorthand.  (This, annoyingly, has nothing to do with the "P!=NP" you may have seen, even though there's an exclamation mark involved.  There's only so many keys on a keyboard so while mathematicians use "!" to mean "factorial" programmers and computer scientists use "!=" to mean "does not equal", we'll come on to that bit later)

So we've got 120 different possible trips...just find the shortest of them, easy, you can probably do that without using your fingers, let alone a computer.

So what about six cities?  Turns out there are 720 trips to test.  OK, it's do-able in your head, but a computer might be helpful.

Seven cities: 5040 trips.

Eight: 40,320

Nine: 362,880

To find the shortest distance between fourteen cities you need to test 87,178,291,200 trips, which is getting a bit silly.  In fact, you very quickly get into the realms of needing a supercomputer, and beyond than even faster.  It's an "NP Complete" problem, and computers hate them.

The big question is, can you find the shortest route another way?  Plenty of people have tried...a particularly cool method is called "ant colony optimization", you write a computer program that simulates ants.  Yes, really, ants.  Each one wanders around between the cities (OK, ant hills) leaving a trail of scent behind it which slowly evaporates.  Whenever an ant reaches an ant hill it follows the path with the strongest scent.  Very quickly you end up with a strong scent trail on what is usually the shortest route.

And therein lies the rub.  Usually.  That doesn't count in maths.  However cool your insect based algorithm is, even if it works 99.999% of the time, it's not a proof.  You can never be sure it's the shortest route without testing it against every possible route, which brings us back to square one and the "computers hate NP Complete problems" thing.

What the P=NP problem really is is the simple question "Is it even possible to find a quicker solution than testing every trip?"

Actually, it's slightly more technical - it asks "If solutions can be checked quickly, can a particular solution be found quickly?".

In the case of the Travelling Salesman this makes a little less sense, but a better example is prime numbers.  Prime numbers can be checked to see if they're really prime quite quickly.  Take 6,538,732,799,420,108,322 for example.  That's a big number, but is it prime?  The answer, fairly obviously, is no.  It ends in a 2, so it's not prime.  That's an example of a really easy check that takes no time at all, we don't have to try dividing it by every possible number because there's a more obvious solution.

Now try finding the next prime number after 6,538,732,799,420,108,322 (without looking it up on the internet...)

Bit trickier huh?

That's a good example of the P=NP problem right there...is there, even in theory, a quicker solution than testing every number bigger than 6,538,732,799,420,108,322 until you find a prime one?  (And trust me, that'll take ages).

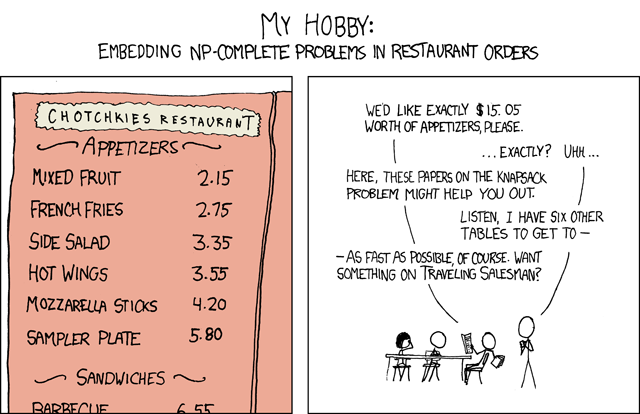Pic courtesy of the wonderful xkcd, by kind permission.

The majority of mathematicians and computer scientists believe, in fact, that P!=NP, that there are some problems you just have to do the long way.  The longest possible way in fact.  And the suggested proof supports this.  If Vinay Deolalikar is correct then several things will happen:

1. He'll win $1,000,000 for cracking one of the Millennium Problems, one of the great mathematical problems of the last few hundred years.  (Another fell in March this year with Grigori Perelman's proof of the Poincare Conjecture)
2. He'll quite possibly win a Fields Medal, the maths equivalent of a Nobel Prize....but only if he's under 40 years old.  
3. The world of cryptography will heave a sigh of relief.
4. There's every likelyhood that the share prices of the major banking electronics companies will peak a little.

Cryptography and banking are the "real world" news here in many ways.  Whenever your bank details or credit card details are sent over the internet there's an NP Complete problem involved.  Your card details are jumbled up using very big prime numbers, and un-jumbling them is very, very nearly an NP Complete problem.  There is a shortcut, but it 100% relies on one little piece of information about how the jumbling was done.


To hack the transmission you either need a copy of the bank's bit of information (a stunningly well guarded and regularly changed bit of information too), or you need to spend several years or even decades with the most expensive computer on the planet running at full whack.  You can do it, but by the time you do the card will have expired.


You can crack bank codes, but it's not worth it.  The question has always hovered though...could some bedroom genius suddenly turn up out of the blue with a quick way to crack it?  If s/he did then secure internet banking as we know it would cease to exist...a replacement would probably be found quite quickly, but the same fear would exist, could the replacement also be cracked at any time?


If P!=NP as suggested then it means there will never be a quick way to break the banks codes.  As computers get faster the banks can simply use bigger and bigger prime numbers, of which there's an infinite number.


Until quantum computers come along at least, but that's a whole other story....

Asus Eee 1001p Review. (Plus a bit of a hack)

So I've finally splashed out on a new computer.  To be honest it's not hugely different to my current machine, a 1.66MHz processor, 1Gb RAM, 140Gb HD, pretty standard gubbins all round in fact.  The big difference is I can lift this one without turning a funny shade of scarlet - it's a netbook, a tiny little Asus Eee 1001p.

Pic from Asus website

It's really pretty cool.  The version I got (from User2, my favourite indy computer shop) came with XP pre-installed, which saw the light of day for about half an hour while I downloaded and installed Ubuntu Netbook Remix.  I'm not normally a fan of "Fisher-Price" style GUIs, normally full of big friendly buttons and presumptions about the user, but UNR is cracking - a pretty much standard version of Ubuntu but nicely optimised for netbooks, especially the wide-but-short screen.  Every single aspect was intuitive and worked straight out of the box except for the wireless (you need to install the ndiswrapper and the original XP driver, there's a guide that shows you how to do it in about five minutes), and the multi-touch trackpad functions, although the side scrolling is fine out of the box, so I'm not especially bothered - Ubuntu hasn't yet caught up with the funkier aspects of touch interfaces yet, but it's only a matter of time.

So it's safe to say I like the OS, even if it's not the one that came with the machine.  Asus don't seem to be making quite such a song and dance about Linux as they did when the original Eee came out, but their website still clearly labels machines as supporting GNU/Linux and given the ease of installation I'm guessing they're still quietly keen on my favourite OS.  To top it all, whilst trying to get into the BIOS I made a little discovery that doesn't seem to be advertised...there's another OS which appears to live on the motherboard - a tiny little linux distro.  That's right, you can pick up all the Windows viruses you want, corrupt whatever you want, hell, you can even wipe the HD....and the machine will still boot to a useable OS with internet support and a frankly rather swish GUI.  In seconds too.  I'm surprised Asus don't make a little more noise about this, it's a wonderful feature.

Hardware wise, it's pretty much faultless considering it's a netbook.  It's respectably quick, you've got all the usual ports, 3x USB, external monitor, MMC-SD slot, ethernet and separate audio in/out sockets.  The HD is big enough for all but the most ardent movie fans and who really cares about optical drives anyway?  Battery life is good - I'm getting a "real" six hours, so Asus' claim of eleven isn't utterly outrageous if you're really careful, and there's a bigger, meaner battery pack available should you feel the need.  Hibernation, previously a problem for many linux distros, works flawlessly.  I've not managed to find out battery life whilst hibernating, but it's "ages" at least.  The matt carbon-fibre style finish is rather funky and prevents the usual smeary finger-prints if that bothers you.

So it's all pretty funky.  Downsides?  Well, the border between the trackpad and the casing isn't particularly tactile, it's easy for your finger to run off the edge leaving you trying to scroll with the case.  A tiny little raised plastic ridge around the trackpad would be a very nice addition to use-ability.  That's about it really...it's difficult to be much more critical without going down the "it's a netbook but I really wanted a laptop!" route.  It does what it says on the tin, and very smoothly indeed.

Which brings us to the bit where I start showing off.  Netbooks are, obviously, quite steal-able objects.  This one could even be hidden in a pocket if you have slightly bigger than average ones, so what to do?  Well, it's not a perfect solution but I rather like it:

Firstly, set up a guest account.  Don't give it a password, make it easy to get in to, it's a honey trap.  Turn off all the admin features etc, but make sure you can still connect to the internet via wireless.

Next, install (sudo apt-get install...) two little programs, fswebcam and googlecl.  The first is a very lightweight command line webcam program, the second is Google's rather natty command line interface.

You'll need a config file for fswebcam, I used this (securesnap.conf):

log /home/guest/.webcamlog.txt
#log /dev/null
device /dev/video0
skip 10
jpeg 80
#deinterlace
resolution 1600x1200
no-banner
set "Sharpness"=200
#set "White Balance Temperature, Auto"=False
set "White Balance Temperature, Auto"=True
set "Backlight Compensation"=0
set "Brightness"=130
set "Contrast"=32
#32 is default
set "Saturation"=28
#28 is default
frames 1
#frames 255
#loop 1


You'll also need the following script:

#!/bin/bash
while [ true ]
do fswebcam -c /home/guest/.security/securesnap.conf
google picasa post --title "Security Shots" /home/guest/.security/output.jpg
rm -f /home/guest/.security/*.jpg
sleep 30
done


Set the second script to run as a startup program when guest logs in, and voila, it takes a photo with the webcam every 30 seconds and uploads them to a picasa account (you need to give it your picasa user name the first time you run it, via terminal).  I can't get it to stop when guest logs out, but that's hardly a big issue.  I'll write an installer to automate it all when I've got time.

CME aimed at Earth

SpaceWeather.com is reporting that the Sun has got a little bit busier recently.  After months of suspiciously quiet behaviour we've had a "complex global eruption".  A sunspot has suddenly flared up, and a filament of material has erupted from the surface.  The two events occurred together, the suggestion being that they are both symptoms of a single event.  The flare and the filiament appear to be separated on the surface by about 45 degrees, meaning it's an event covering a substantial proportion of the Sun's surface.

To top it all the SOHO satellite has filmed a Coronal Mass Ejection (CME) aimed squarely at Earth.  A CME is basically a lump of Sun-stuff, a very thin, very hot plasma, being flung out from the Sun at very high speed indeed.  This one should reach us sometime on the evening of the 3rd of August.

Don't Panic.

This is a relatively small CME, and will probably just give those of us in the northern part of the globe some rather pretty aurora.  Maybe more, it's not inconceivable that there will be a little disruption in communications if satellites have to shut down to protect themselves, but please don't go believing any apocalyptic 2012 nonsense you hear.

Anyway, we've all got a Zombie Plan, haven't we? ;)